A7 – Enhancement in the Frequency Domain

Filtering in Fourier Space
"Unwanted repetitive patterns in an image can be removed by masking their
frequencies in the Fourier domain. Alternatively, desired frequencies in the image
may also be enhanced."

A Convolution Theorem

Figure 1.Results for steps 1 to 3.

Figure 2. Variance

As you vary the variance the FT intensity changes in such a way that increasing the variance increase the radius of the FT.

Fig 3. Inversion

To invert the gaussian dots such that highest becomes 0, lowest becomes 255
or 1.0 , I just multiplied the original values by -1 *255 and then added 255.

B. Fingerprints : Ridge Enhancement

Fig 4. The problem

After converting the image to grayscale, I took the FFT and from here try to create a mask to remove the frequencies of the blotches which is ... unknown.
So what I did is start by removing the higher frequencies...obviously using a circular aperture didnt work as seen in Fig.5.

Fig 5. Removing the higher frequencies with a circular aperture... didnt work

Next I tried the other way around, I didnt mask the higher frquencies but just retained it, then I tried cleaning the frequencies close the center as shown in Fig 6 until I finally tried creating a mask from the FT and just clean the FT as shown in Fig 7. The final almost cleaned finger print is shown in Fig 6 (last).

Figure 5.
Figure 6.

before(original fingerprint)
after-the enhanced fingerprint with ridges more clear and less blotches. This final image is from Figure 6c.

C. Lunar Landing Scanned Pictures : Line removal
Remove the vertical lines in the image by filtering in the Fourier Domain.

Fig 7. Lunar image with vertical lines

a. b.

Fig 8. a.FT and horizontal mask to remove the vertical lines. b. the FFT of thw masked FT, the final image is inverted with no more vertical lines.

Fig. 9. The final cleaned image after rotation.

D Canvas Weave Modeling and Removal

Fig. 10 The canvas with weave pattern

Fig 11. The graycale of canvas image

Figure 12.FT of the image

Fig 12. Tried a combination of gaussian filtering and masking the regions shown in c... didint work , the resulting image in e was too blurred.

Figure 13. Made a mask that removes the symmetric peaks around the center.

The mask in figure 13 b, removed the frequencies of the weave pattern and a cleaned image is retrieved by taking the FT again. Also, the cleaned image has higher contrast such that the brushstrokes are enhanced.

Fig. 14. The unwanted canvas weave pattern is now removed(im from Fig 13 c).

Fig. 14. The inverted mask of the peaks

Fig. 15. The FT of inverted mask. It does look like the canvas weave pattern.

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Code:

a.Variance =2^2

b.Variance=3^2

nx = 100; ny = 100;

x = linspace(-100,1,nx);

y = linspace(-100,1,ny);

[X,Y] = ndgrid(x,y);

s1=4;//variance 1

s2=9;//variance 2

h=scf(1);

z1 = exp((-1*(sqrt((X+50).^2+(Y+50).^2)))/s1);

imshow(z1);

//xs2gif(1,'variance1.gif');

h=scf(2);

ft1=fftshift(abs(fft2(z1)));

imshow(ft1);

h=scf(3);

z2=exp((-1*(sqrt((X+50).^2+(Y+50).^2)))/s2);

imshow(z2);

//xs2gif(2,'variance2.gif');

h=scf(4);

ft2=fftshift(abs(fft2(z2)));

imshow(ft2);

A6 – Properties of the 2D Fourier Transform

A .Familiarization with FT of different 2D patterns

Figure 1. a FFT of a circle, b. shifted FFT and c. FFT of FT resulting to the same circle.

Figure 2.

For Fig.2, the images above starting from the left are namely, an annulus, a square, square annulus, 2 slits and 2 dots all representing what we call apertures. The images on the bottom are their corresponding FT which is an Airy pattern for the annulus, a sinc function for the square apertures, double slit diffraction of maxima and minima in the horizontal axis for the vertical slits ans the sinusoid for the two dots.

a. b. c. d.

Figure 3. Comparison of a circular annulus and square annulus.

As expected the we have the a Airy pattern for a,b and a sinc function for c,d.
From these results we can say that the size of the aperture determines the intensity of the resulting diffraction pattern. It can be seen that the smaller the aperture is the brighter or more intense the FT or diffraction pattern is.

Figure 4. Variation in the dot size or pinhole radii

IT is shown in Fig.3 that the FT of 2 dots is a superposition of the FT of 2 small dots and FT of a circular aperture.



B Anamorphic property of the Fourier Transform

Anamorphic means something like producing different imaging effects along mutually perpendicular radii. We can see these in FT of perpendicular sinusoid signals.

Figure 5. Increase in the frquency

Increasing the frequency of the signal(sinusoid) resulted to the increase in the separation of the dots. We see here that the two dots corresponding to the frquency peaks shifted farther and father from the center, such that the lower the frequency the closer it is to the center while farther at higher frequency. The same with interferograms ,the spacing between the peaks of the FT of the signal gives corresponding frequency of the signal.

Fig.6 Effect of biasing

For a sinusoid of constant frequency and orientation, we expect that the peaks of the FT to remain the same since and it did and the position of the peaks did not vary. However the intensity of the dots was observe to change such that at low biasing the outer peaks were brighter and reduced at higher biasing which made (m=0) the central maximum peak brightest.

Fig.7

Since adding or subtracting the bias didn’t affect position of the peaks of the FT of the signal , we can just to choose to add the bias . For frequency=4, bias=0.1,1,10,100 was added to the sine wave and the resulting FT of the signal show that the only the intensity of the peaks varied and not the spacing.

Fig. 8

Rotating the signal(sinusoid) by an angle results to the rotation of the peaks of the FT.

Fig. 9

Top image shows the pattern and below is its Fourier transform .Now the combination of these sinusoids in X and Y with the formula

z = sin(2*%pi*4*X).*sin(2*%pi*4*Y);

has a FT that is again symmetric about the center and with peaks that correspond to the frequency of each sinusoid in their respective axis. The combined signal had the same frequency as illustrated in their perfect symmetry but once we changed one of the frequency of the signals, say in the X axis,

z4 = sin(2*%pi*8*X).*sin(2*%pi*4*Y);

the x separation in the vertical orientation increased. We recall that the higher the frequency the farther the peak from the center.

Fig 10

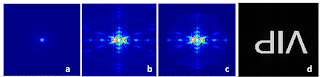
Addition of the combined sinusoids in the X and Y axis to 2 rotated sinusoids (theta=40,60deg) resulted to the image illustrated on top. Below is its FT which by inspection, is just the sum of the FT of each signal. The FT is thus useful for decomposing the frequency component in sampled signals.

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Activity 5 Fourier transformers!

-busy ang neurons...

Lens as Fourier Transformer

6.A – Familiarization with discrete FFT



Figure 1.



Figure 2.




Figure 3.



6.B Simulation of an imaging device


Figure 4.



Figure 5.


Figure 6.


6.C Template Matching using correlation

Figure 7.



Figure 8.


Figure 9.



Figure 10.



Figure 11.



6.D Edge detection using the convolution integral


Figure 12.